Question

The ratio of the base edges of two similar pyramids is 3:4. The volume of the larger pyramid is 320 in3. What is the volume of the smaller pyramid?

240 in3
189 in3
135 in3
180 in3

Answer 1

use similar volume to calculate
which is the (ratio of edges)^3 = (ration of volume)
so just put the numbers in, let the volume of smaller pyramid be y.
(3/4)^3 = y/320
27/64 = y/320
y=135in3

Answer 2

Option C. 135 in³

Explanation:

Since volume is a three dimensional unit in which three dimensions of any object is multiplied.

If the sides of two similar pyramids are in the ratio of
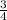`(3)/(4)`, ratio of their volume will be =
`((3)/(4))^(3)`

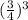
Which clearly says that

`\frac{\text{Volume of smaller pyramid}}{\text{Volume of large pyramid}}=((3)/(4))^(3)`

`\frac{\text{Volume of smaller pyramid}}{\text{Volume of large pyramid}}=(27)/(64)`

`\frac{\text{Volume of smaller pyramid}}{320}=(27)/(64)`

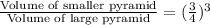
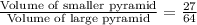
Volume of the smaller pyramid =
`((320)(27))/(64)=135`

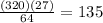
Therefore, volume of the smaller pyramid is 135 in³

Option C. 135 in³ is the correct answer.