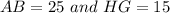Question

To prove that the triangles are similar by the SSS similarity theorem, it needs to be shown that...

AB = 25 and HG = 15
AB = 30 and HG = 18
AB = 35 and HG = 21
AB = 35 and HG = 15

Answer 1

we know that

The SSS similarity theorem states that if the ratios comparing the corresponding sides of two triangles are all equal, then the two triangles are similar.

So

in this problem

the corresponding sides are

AB and HG

BC and HI

AC and GI

Step
`1`

Find the value of side AB

Applying the Pythagorean Theorem

`AB^(2) =AC^(2) +BC^(2) \\ AB^(2) =15^(2) +20^(2)\\ AB^(2) =625\\ AB=√(625) \\ AB=25\ units`

Step
`2`

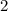
Find the value of side HG

Applying the Pythagorean Theorem

`HG^(2) =HI^(2) +IG^(2) \\ HG^(2) =12^(2) +9^(2)\\ HG^(2) =225\\ HG=√(225) \\ HG=15\ units`

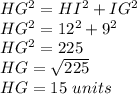
Step
`3`

Compare the ratios of the corresponding sides

`(AB)/(HG) =(25)/(15) =(5)/(3) \\ \\`

`(BC)/(HI) =(20)/(12) =(5)/(3) \\ \\`

`(AC)/(GI) =(15)/(9) =(5)/(3) \\ \\`

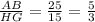
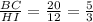
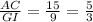
The ratios comparing the corresponding sides of two triangles are all equal, then the two triangles are similar

therefore

the answer is the option

`AB = 25\ and\ HG = 15`

Answer 2

by Pythagoras Theorem,

AB =
`\sqrt{15^(2)+ 20^(2) } =25`

HG =
`\sqrt{ 12^(2) + 9^(2) }=15`

The scale factor of each corresponding side is

`(AC)/(HI)= (CB)/(IG)= (AB)/(HG) = (5)/(3)`

The two triangles are similar by SSS

The correct answer is the option number 4