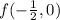The given expression is
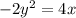
If we rewrite this expression, it would be
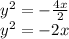
Or, we can rewrite this way too
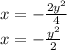
As you can observe, the quadratic variable is
 not
not
 , this change the orientation of the figure. Actually, this change a lot, because this parabola doesn't represent a function, because it will open horizontally, specifically, towards negative infinte, like the image attached shows.
, this change the orientation of the figure. Actually, this change a lot, because this parabola doesn't represent a function, because it will open horizontally, specifically, towards negative infinte, like the image attached shows.
If you do the vertical line test, you will see that such vertical line intercepts the figure in two points, which indicates that it's not a function.
Now, in this case, the directrix is defined as
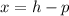 , because the parabola is horizontal. Where
, because the parabola is horizontal. Where
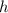 is the horizontal coordinate of the vertex, and
is the horizontal coordinate of the vertex, and
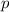 can be found as follows.
can be found as follows.
When, the parabola is horizontal is defined as
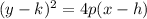
Where
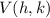 are the coordinates of the vertex, which in this case is
are the coordinates of the vertex, which in this case is
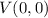 . Also, particularly, we have that
. Also, particularly, we have that
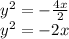
So,
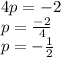
Then, the directrix would be
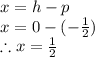
And the focus is defined as
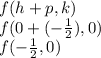
Therefore, the asnwer are
- This parabola opens to the negative x-axis, as the image shows.
- The equation of the directrix is:
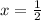
- The focus of the parabola is at: