Question

Explain why rational exponenets are not defined when the denominator of the exponent in lowest terms is even and the base is negative. << Read Less

Answer 1

Recall that one of the rules of exponents states that

`x^{ (m)/(n) }= \left(\sqrt[n]{x} \right)^m`

Now, let x be a negative number and n, an even number, then

`(-x)^{ (m)/(n) }= \left(\sqrt[n]{(-x)} \right)^m`

But the even root of a negative number is not a real number.
for example,
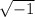
`√(-1)` is not a real number, rather a complex number.

Hence, rational exponents are not defined when the denominator of the exponent in lowest terms is even and the base is negative.