Answer: The sum would be 1173.3333....
Explanation:
Since we have given that
a₁ = 880
r =

We need to find the sum in sigma notation;
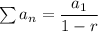
And we need to calculate the sum that will be the upper limit of this population:

Hence, the sum would be 1173.3333....