Question

suppose you want to make an open topped box out of 4x6 index card by cutting a square out of each corner and then folding the edges. how large a square should you cut out of each corner in order to maximize the volume of the resulting box

Answer 1

To maximize the volume of an open-topped box from an index card, you need to use calculus to find the optimal size of the square to cut from each corner. The volume function V = x(4-2x)(6-2x) should be optimized by taking its derivative and finding the critical points where the derivative equals zero.

Step-by-step explanation:

To maximize the volume of an open-topped box created from a 4x6 index card by cutting out squares from each corner, we must define a variable for the square cut out. Let the side of the square cut from each corner be x. The new dimensions of the box will be (4-2x) by (6-2x) with a height of x. The volume V of the box is then given by V = x(4-2x)(6-2x).

To find the value of x that maximizes volume, we would take the derivative of the volume function with respect to x and set it to zero. Finding the critical points will let us know the value of x that gives the maximum volume. To solve this optimization problem, we use calculus methods. Unfortunately, without the precise calculations this answer will not be complete.

Answer 2

so check the picture below

notice, since you're cutting out a square, the sides must all be equal, thus the largest "x" can't be 2, half of 4, it has to be just less than 2 or it has no volume, so x<2, and can't be 0, because, you'd have no volume either, so x>0, so 0<x<2


`\bf V=(4-2x)(x)(6-2x)\implies V=(4x-2x^2)(6-2x) \\\\\\ V=4x^3-20x^2+24x \\\\\\ \cfrac{dv}{dx}=12x^2-40x+24\implies 0=12x^2-40x+24 \\\\\\ 0=3x^2-10x+6`

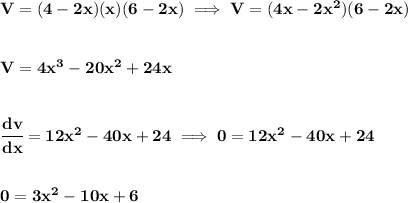
anyway... so that'd be dv/dx... you can just run it through the quadratic formula to get the critical points, and run a first-derivative test on them, bearing in mind the range for "x", (0, 2)