Question

Identify the axis of symmetry and vertex of f(x) = –2x2 –2x–1.

Answer 1

Part A) The vertex is the point
`(-0.5,-0.5)`

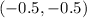
Part B) The axis of symmetry is
`x=-0.5`

Explanation:

we know that

The equation of a vertical parabola into vertex form is equal to

`y=a(x-h)^(2)+k`

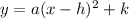
where

(h,k) is the vertex of the parabola

and the axis of symmetry is equal to the x-coordinate of the vertex

so

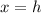`x=h` -----> equation of the axis of symmetry

In this problem we have

`f(x)=-2x^(2)-2x-1`

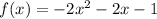
Convert to vertex form

Group terms that contain the same variable, and move the constant to the opposite side of the equation

`f(x)+1=-2x^(2)-2x`

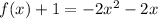
Factor the leading coefficient

`f(x)+1=-2(x^(2)+x)`

Complete the square. Remember to balance the equation by adding the same constants to each side

`f(x)+1-(1/2)=-2(x^(2)+x+(1/4))`

`f(x)+(1/2)=-2(x^(2)+x+(1/4))`

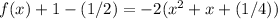
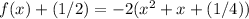
Rewrite as perfect squares

`f(x)+(1/2)=-2(x+(1/2))^(2)`

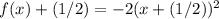
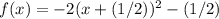`f(x)=-2(x+(1/2))^(2)-(1/2)` -----> equation in vertex form

The vertex of the parabola is the point
`(-0.5,-0.5)`

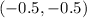
Is a vertical parabola open downward

The axis of symmetry is equal to

`x=-0.5`

see the attached figure to better understand the problem

Answer 2

Given the quadratic equation: f(x) = -2x^2 - 2x - 1, the axis of symmetry can be obtained by finding the line that divides the function into two congruent or identical halves. Thus, it should pass through the vertex and is equal to the x-coordinate of the vertex.

Note that a quadratic equation in standard form: y = ax^2 + bx + c, has the vertex located at (h,k) where, h = -b/2a and k is determined by evaluating y at h. In this case, a = -2, b = -2, thus, h = -0.5, k = 0.5. Thus, the vertex is located at (-0.5, 0.5) and the axis of symmetry is at x = -0.5.