Question

Solve in 5 + in (2x) = 5

Answer 1

remember

ln(x) is
`log_e(x)`
and

`log_a(b)=c` translates to

`a^c=b`
and
log(a)+log(b)=log(ab)

so

ln5+ln(2x)=5 means
ln(5*2x)=5 or
ln10x=5
translate, base e
e^5=10x
divide both sides by 10

`(e^5)/(10)=x`
that's about 14.94

Answer 2

`x = (e^5)/(10)`

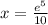
Explanation:

Assuming that we have the following question:

`ln (5) + ln(2x) = 5`

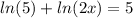
We can use the following property assuming that we have the same base for the logarithm:

`Log(a*b) = Log(a) Log(b)`

And if we use this we got:

`ln(5*2x ) = ln(10x) = 5`

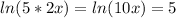
Now we need to remember that the inverse operation for the natural log is the exponentiation so we can do this on both sides in oder to remov the natural log:

`e^(ln(10x)) = e^5`

`10 x = e^5`

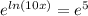
And then we can divide both sides by 10 and we got:

`x = (e^5)/(10)`

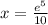
And that would be our final answer for this case.