Question

Can anyone explain this step by step? More specifically this part. I'm working on logarithmic differentiation to find dy/dx of y=square root x(x+2)

Answer 1

`y=√(x(x+2))=\sqrt x√(x+2)=x^(1/2)(x+2)^(1/2)`

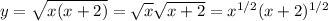
Take the logarithm of both sides.


`\ln y=\ln(x^(1/2)(x+2)^(1/2))=\frac12\ln x+\frac12\ln(x+2)`

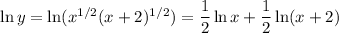
In the last equality, we used the fact that
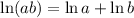
`\ln(ab)=\ln a+\ln b` and
`\ln a^c=c\ln a`.

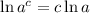
Differentiating both sides with respect to
`x`, we have


`\frac1y(\mathrm dy)/(\mathrm dx)=\frac1{2x}+\frac1{2(x+2)}`

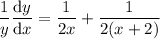
where the left hand side occurs by the chain rule (recall that
`y` is a function of
`x`).

The solution then follows from the steps in your attachment, which is just a matter of algebraic manipulation.