Question

Simple Cuts is a hair salon that offers two types of haircuts: a buzz cut and a flat-top. Jerry charges $9 for a buzz cut and $13 for a flat-top. If Jerry made $600 one day and knows that he cut three times as many buzzes as flat-tops, how many flat-tops did he cut that day?

Answer 1

Let x=the number of Buzz & let y = number of flat:

9x+13y = 600

But 3x = y (given) then ==> 9x+(13)3x= 600==48x =600 x = 12.5

& y=37.5 (PROOF 9 x 12.5) + (13 x 37.5) =600

Answer 2

well hmmm
let's say
b = amount of buzz cuts
f = amount of flat-top cuts

now, the total price for all the buzz cuts, since each one is $9, will then be 9*b or 9b

and the price for all flat-top cuts, since each is $13, will then be 13*f or 13f

one day Jerry made a total of $600, so we know, whatever "b" and "f" are, we know their price sum was 600,

thus 9b + 13f = 600

now, Jerry "knows that he cut three times as many buzzes as flat-tops", so, whatever "f" is, "b" is three times that much, or 3*f, so b = 3f

now then
`\bf \begin{cases} 9b+13f=600\\ \boxed{b}=3f\\ ----------\\ 9\left( \boxed{3f} \right)+13f=600 \end{cases}`

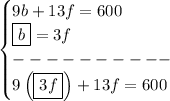
solve for "f"