Question

At most, Alana can spend $40 on carnival tickets. Ride tickets cost $4 each, and food tickets cost $2 each. Alana buys at least 16 tickets. The system of inequalities represents the number of ride tickets, r, and the number of food tickets, f, she buys.

r + f ≥ 16
4r + 2f ≤ 40
What is the maximum number of ride tickets she can buy?
4
6
10
12

Answer 1

on Ed the answer is A

Answer 2

Option A is correct

4 is the maximum number of ride tickets she can buy

Step-by-step explanation:

Here, r represents the number of ride tickets and f represents number of food tickets.

The system of inequalities is given as:

`r+f\geq 16` ....[1]

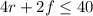`4r+2f\leq 40` .....[2]

To solve Mathematically:

Multiply equation [1] by -2 we have;

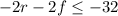`-2r-2f \leq -32` .....[3]

Add equation [2] and [3] we have;

`2r \leq 8`

Divide both sides by 2 we have;

`r \leq 4`

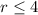
Since, r must be less than or equal to 4.

You can also see the graph of the given system of inequalities as shown below.

The intersection point is, (4, 12)

Therefore, the maximum number of ride tickets she can buy is, 4.