Question

Betty correctly determined that the ordered pair (–3, 5) is a solution to the system of linear equations and x + 4y = 17. Based on this information, which statement is correct? (–3, 5) satisfies neither the equation 6x + 5y = 7 nor the equation x + 4y = 17. (–3, 5) satisfies the equation 6x + 5y = 7 but not the equation x + 4y = 17. (–3, 5) satisfies the equation x + 4y = 17 but not the equation 6x + 5y = 7. (–3, 5) satisfies both the equation 6x + 5y = 7 and the equation x + 4y = 17.

Answer 1

5) satisfies both the equation 6x + 5y = 7 and the equation x + 4y = 17 <-----answer

Answer 2

D. (–3, 5) satisfies both the equation 6x + 5y = 7 and the equation x + 4y = 17.

Explanation:

The given equations are:

`6x +5y=7`

and

`x+4y=17`

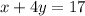
Betty correctly determined that the ordered pair
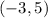`(-3,5)` is a solution by substituting it into both equations.

Betty's work will look like this;

First Equation:

`6(-3) +5(5)=7`

`-18 +25=7`

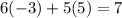
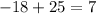
This statement is True.

Second equation;

`-3+4(5)=17`

`-3+20=17`

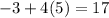
This is also TRUE

Hence the correct answer is

D. (–3, 5) satisfies both the equation 6x + 5y = 7 and the equation x + 4y = 17.