Question

For what interval is the value of (f-g)(x) negative?

Answer 1

First find (f-g)(x)

(f-g)(x)=x-3--0.5x

(f-g)(x)=x-3+0.5x

(f-g)(x)=1.5x-3

Now we want to know when (f-g)(x)<0 so:

1.5x-3<0

1.5x<3

x<2 so the interval when (f-g)(x)<0 is:

(-oo, 2)

Answer 2

(-∞,2)

Explanation:

Given : f(x)=x-3

g(x)= - 0.5x

To Find : For what interval is the value of (f-g)(x) negative?

Solution :

First calculate the (f-g)(x)

Since f(x)=x-3

g(x)= - 0.5x

So, (f-g)(x) = x-3-(- 0.5x)

⇒(f-g)(x) = x-3+ 0.5x

⇒(f-g)(x) =1.5x-3

Now we are supposed to find the interval for which (f-g)(x) is negative.

So, (f-g)(x) =1.5x-3 <0

⇒1.5x<3

⇒
`x<(3)/(1.5)`

⇒
`x<2`

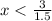
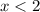
Thus for (f-g)(x) negative x must be less than 2

Thus the interval is(-∞,2)

Hence option B is correct