Question

Is each line parallel, perpendicular, or neither parallel nor perpendicular to a line whose slope is −6?

Drag each choice into the boxes to correctly complete the table.

Answer 1

line M with slope 6 is neither, line n with slope -6 is parallel because only lines with same slope are parallel, line p with slope 1/6 is neither. and line q with slope -1/6 is perpendicular because only the reciprocal of a slope is perpendicular, so reciprocal of 6= 1/6 reciprocal of -6=-1/6 reciprocal of 2= 1/2

Answer 2

we have

the slope of the given line is

`m1=-6`

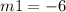
we know that

If two lines are parallel , then their slopes are the same

so

`m1=m2`

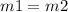
if two lines are perpendicular, then the product of their slopes is equal to minus one

so

`m1*m2=-1`

we will proceed to verify each case to determine the solution

case A) line m with slope
`6`

Compare the slope of the line m of the case A) with the slope of the given line

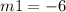`m1=-6` -----> slope given line

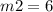`m2=6` ----> slope line m case A)

`m1\\eq m2`

`m1*m2\\eq-1`

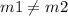
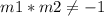
therefore

the line m case A) and the given line are neither parallel nor perpendicular

case B) line n with slope
`-6`

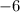
Compare the slope of the line n of the case B) with the slope of the given line

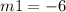`m1=-6` -----> slope given line

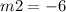`m2=-6` ----> slope line n case B)

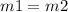`m1=m2` ------> the lines are parallel

case C) line p with slope
`(1)/(6)`

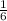
Compare the slope of the line p of the case C) with the slope of the given line

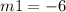`m1=-6` -----> slope given line

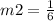`m2=(1)/(6)` ----> slope line p case C)

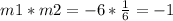`m1*m2=-6*(1)/(6)=-1` ------> the lines are perpendicular

case D) line q with slope
`-(1)/(6)`

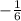
Compare the slope of the line q of the case D) with the slope of the given line

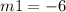`m1=-6` -----> slope given line

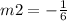`m2=-(1)/(6)` ----> slope line q case D)

`m1\\eq m2`

`m1*m2\\eq-1`

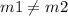
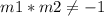
therefore

the line q case D) and the given line are neither parallel nor perpendicular

the answer in the attached figure