Question

Secxtanx(1-sin^2x)= x

Answer 1

Recall that the secant function is the reciprocal function to the cosine function.
Also, recall that sin²x + cos²x = 1 and 1 - sin²x = cos²x

Thus, we can rewrite the equation as:

`(tan(x) \cdot cos^(2)(x))/(cos(x)) = x`

`tan(x) \cdot cos(x) = x`

`(sin(x) \cdot cos(x))/(cos(x)) = x`

`sin(x) = x`

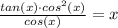
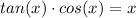
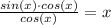
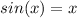
There's only one point at which sin(x) = x, and that's at x = 0.

Thus, x = 0 is the only solution.

Answer 2

Answer: sin

Explanation:

Just took this on A Pex You’re welcome. I got it correct when I put sin in the blank before the x