First note that
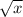
is only defined for

when
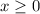
, and that
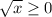
as a consequence.
This means the equation actually has no real solutions, so if algebraically manipulating the equation does yield a real solution, it must necessarily be extraneous. Let's see what happens.
Squaring both sides, we get
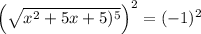
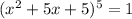
Take the (real-valued) fifth root of both sides:
![\sqrt[5]{(x^2+5x+5)^5}=\sqrt[5]1](https://img.qammunity.org/2018/formulas/mathematics/high-school/f6k0a7d27oemuf1ns79xuabuxk8mk6acqh.png)
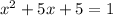
Now solve for

.
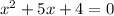


But as I pointed out earlier, these must be extraneous. Plug them into the equation to check:
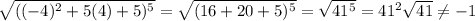
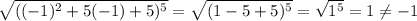
This means the answer is A.