Question

Derive the equation of the parabola with a focus at (0, 1) and a directrix of y = −1?

Answer 1

so hmm notice the picture below

keep in mind that, the vertex is half-way between the focus point, and the directrix

so.. since the focus is up, and the directrix, down below, that means, the parabola is vertical and opening upwards, thus the squared variable is the "x"

thus
`\bf \begin{array}{llll} (y-{{ k}})^2=4{{ p}}(x-{{ h}}) \\\\ \boxed{(x-{{ h}})^2=4{{ p}}(y-{{ k}})}\\ \end{array} \qquad \begin{array}{llll} vertex\ ({{ h}},{{ k}})\\\\ {{ p}}=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix} \end{array}`

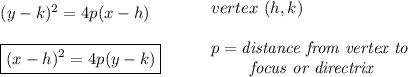
so.. from half-way of the focus and directrix, you can see what h,k coordinates are for the vertex, and you can also see the "p" distance from the vertex to either, the focus or directrix

so... just plug in those values

Answer 2

(03.09 MC)

Derive the equation of the parabola with a focus at (0, 1) and a directrix of y = −1. (2 points)

f(x) = − x2

f(x) = x2

f(x) = −4x2

f(x) = 4x2

answer: f(x) = 1/4 x2