Answer: The correct option is (A) 7.
Step-by-step explanation: Given that a bag contains 18 blocks numbered from 1 to 18. Two blocks are selected from the bag at the same time.
Let, E = even that the two numbers differ by 11.
Is 'S' is the complete sample space for the event of selecting two blocks, then
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (1, 7), (1, 8), . . , (17, 18), (18, 18)}.
The number of elements of the sample space 'S' is
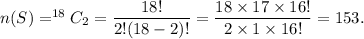
The event 'E' is a subset of the above sample space 'S'.
We are to find the number of outcomes of the event 'E'.
Since 'E' is the event such that the two numbers differ by 11, so
E = {(1, 12), (2, 13), (3, 14), (4, 15), (5, 16), (6, 17), (7, 18)}.
Therefore, n(E) = 7. That is, there are 7 outcomes in event 'E'.
Thus, the correct option is (A). 7.