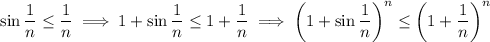
You know the right side converges to

as
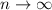
, so
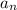
is bounded from above.
Now,
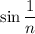
on its own is a monotonically decreasing sequence approaching 0, which means
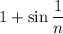
approaches 1 from above, i.e.
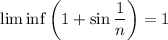
. For all intents and purposes, you can basically think of
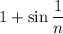
as a number larger than 1; call it
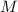
. For all
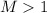
, you have
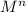
a positive, strictly increasing sequence. It follows, then, that
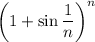
must be a strictly increasing sequence.
Therefore
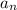
must converge to

by the monotone convergence theorem.