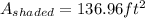Question

A triangle is inside a circle where the triangle's base is on the circle's diameter as shown.

What is the area of the shaded region?

Use 3.14 for π .

Enter your answer as a decimal in the box.

Answer 1

area of a circle=pi x r^2= 3.14 x 8^2(half of the radius)=3.14 x 64=200.96

area of triangle= 1/2 bh=1/2(16)(8)=1/2(128)=64

200.96-64=136.96 sq.ft

Answer 2

`A_(shaded)= 136.96 ft^(2)`

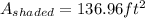
Explanation:

We will find the shaded area if we subtract the area of the triangle from the area of the circle.

We know that the area of the circle is defined as

`A= \pi r^(2)`

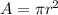
Where
`r` is half the diameter, that is

`r=(16ft)/(2)=8ft`

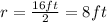
The area of the circle is

`A= \pi r^(2)\\A= 3.14 (8ft)^(2) =200.96ft^(2)`

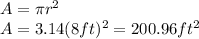
Now, we have to find the area of the triangle, which is defined as

`A_(\triangle) =(bh)/(2)`

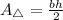
Where
`b` is the base of 16 feet, and
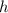`h` is the height of the triangle which is on the radius. So, we have
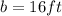`b=16ft` and
`h=8ft`.

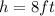The area of the triangle is

`A_(\triangle) =(16ft(8ft))/(2)=64ft^(2)`

Now, the shaded is the difference as we said before, that is

`A_(shaded)=A-A_(\triangle)`

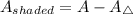
Replacing both areas, we have

`A_(shaded)=200.96 ft^(2) - 64ft^(2)= 136.96 ft^(2)`

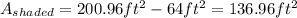
Therefore, the shaded area is
`A_(shaded)= 136.96 ft^(2)`