Differential Equations - Reduction of order given xy'' - (2x+ 1)y' +2y=0 , where y1 = e^(2x)

Question

Differential Equations - Reduction of order

given
`xy'' - (2x+ 1)y' +2y=0` , where y1 =
`e^(2x)`

Answer 1

With reduction of order, we assume a solution of the form
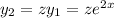
`y_2=zy_1=ze^(2x)`, with
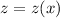
`z=z(x)`. Then


`{y_2}'=(z'+2z)e^(2x)`

`{y_2}''=(z''+4z'+4z)e^(2x)`

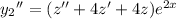
and substituting into the ODE gives


`x(z''+4z'+4z)e^(2x)-(2x+1)(z'+2z)e^(2x)+2ze^(2x)=0`

`x(z''+4z'+4z)-(2x+1)(z'+2z)+2z=0`

`xz''+(2x-1)z'=0`

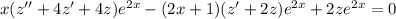
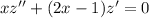
Let
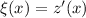
`\xi(x)=z'(x)`, so that
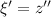
`\xi'=z''`. This gives the linear ODE


`x\xi'+(2x-1)\xi=0`

This equation is also separable, so you can write


`(\xi')/(\xi)=\frac{1-2x}x`

Integrating both sides with respect to
`x` gives


`\ln|\xi|=-2x+\ln x+C_1`

`\xi=C_1xe^(-2x)`

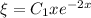
Next, solve
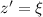
`z'=\xi` for
`z` by integrating both sides again with respect to
`x`.


`z'=\xi`

`\implies z=\displaystyle\int C_1xe^(-2x)\,\mathrm dx`

`\implies z=C_1e^(-2x)(2x+1)+C_2`

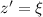
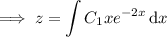
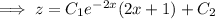
And finally, solve for
`y_2`.


`y_2=zy_1=C_1(2x+1)+C_2e^(2x)`

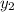
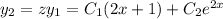
and note that
`y_1` is already taken into account as part of
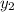
`y_2`, so this is the general solution to the ODE.