Question

Find the vertex, focus, directrix, and focal width of the parabola. x2 = 28y

Answer 1

x^2 = 28y
(x - 0)^2 = 4*7 (y - 0)
a = 7

Answer 2

The general equation of parabola is given by:

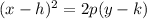`(x-h)^2 =2p(y-k)` ....[1]

where,

vertex = (h, k)

Focus = (0, p/2)

directrix : y = -p/2

and

p represents the focal width

Given the parabola:

`x^2=28y`

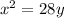
On comparing with [1] we have;

h=k =0

Vertex=(0, 0)

and

2p = 28

Divide both sides by 2 we have;

p = 14

Focus = (0, 14/2)

⇒Focus= (0, 7)

Directrix:

y = -14/2

⇒y = -7

Therefore, the equation of parabola
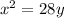`x^2=28y` has

vertex = (0, 0)

focus = (0, 7)

directrix: y = -7

Focal width = 14