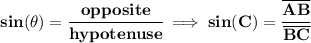Question

Find the measure of ∠C to the nearest degree.

Answer 1

well, sine is
`\bf sin(\theta)=\cfrac{opposite}{hypotenuse}`,

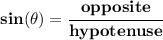
but from the angle C, the opposite side, the one facing it off, is the side
AB, and we dunno what the side AB is

however, we know the hypotenuse is 8, and the adjacent side is 7,

and is right-triangle, thus, let us use the pythagorean theorem,


`\bf c^2=a^2+b^2\implies √(c^2-a^2)=b\qquad \begin{cases} c=hypotenuse\\ a=adjacent\\ b=opposite \end{cases} \\\\ thus \\\\ √(8^2-7^2)=b=AB`

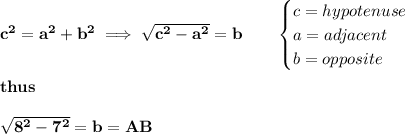
now, that we know what the opposite side is, that is AB, then
we can find the sine of angle C
`\bf sin(\theta)=\cfrac{opposite}{hypotenuse}\implies sin(C)=\cfrac{\overline{AB}}{\overline{BC}}`

Answer 2

`\angle C=28.95502437$^(\circ) \approx29 $^(\circ)`

Explanation:

Let's call the missing side c. And let's find it using pythagorean theorem:

`b^2=c^2+a^2`

Where:

`a=7\\\\and\\\\b=8`

Solving for c:

`c^2=8^2-7^2\\\\c^2=64-49\\\\c^2=15\\\\c=√(15)`

Using law of sines:

`(a)/(sin(A)) =(b)/(sin(B)) =(c)/(sin(C))`

Where:

`B=90`

Solving for C:

`b*sin(C)=c*sin(B)\\\\8sin(C)=√(15) sin(90)\\\\sin(C)=(√(15) )/(8) \\\\C=arcsin((√(15) )/(8) )\\\\C=28.95502437$^(\circ) \approx 29$^(\circ)`