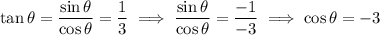Question

The line with equation −a+3b=0 coincides with the terminal side of an angle θ in standard position and sinθ<0 .

What is the value of cosθ ?

Answer 1

-310√10

Explanation:

Answer 2

If
`a` is the variable of the horizontal axis, then you can solve for
`b` to get the equation of the line in slope-intercept form in the
`a,b` plane:


`-a+3b=0\implies b=\frac a3`

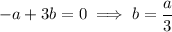
i.e. a line with slope
`\frac13` through the origin, which means it is contained in the first and third quadrants. Since the terminal side of
`\theta` has a negative sine, the angle must lie in the third quadrant.

Because the slope of the line is
`\frac13`, you can choose any length along the line to make up the hypotenuse of a right triangle with reference angle
`\theta`. Any such right triangle will have
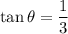
`\tan\theta=\frac13`, regardless of whether the angle is the first or third quadrant. But since
`\theta` is known to lie in the third quadrant, and so
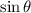
`\sin\theta` and
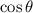
`\cos\theta` are both negative, you have


`\tan\theta=(\sin\theta)/(\cos\theta)=\frac13\implies (\sin\theta)/(\cos\theta)=(-1)/(-3)\implies \cos\theta=-3`