Question

Which equation represents an exponential function that passes through the point (2, 36)?

f(x) = 4(3)x

f(x) = 4(x)3

f(x) = 6(3)x

f(x) = 6(x)3

Answer 1

Option A. is the answer.

Explanation:

In this question we can get the correct option by plugging in the coordinates of point (2, 36) in the functions given in all options.

Option A.

`f(x)=4(3)^(x)`

For (2, 36),

`36=4(3)^(2)`

36 = 4×9

36 = 36

It's true so the function passes through the point (2, 36).

Option B.

`f(x)=4(x)^(3)`

For, (2, 36)

`36=4(2)^(3)`

36 = 4×8

36 = 32

Which is not true.

Therefore, option B is not the answer.

Option C.

`f(x)=6(3)^(x)`

For(2, 36)

`36=6(3)^(2)`

36 = 6×9

36 = 54

It's not true.

Therefore, option C is not the nswer.

Option D.

`f(x)=6(x)^(3)`

For (2, 36),

`36=6(2)^(3)`

36 = 6×9

36 = 54

Which is not true.

Therefore, option D is not the answer.

Answer 2

The exponential function that passes through (2,36) is:

`f(x)=4* 3^x`.

Explanation:

We are asked to find which function passes through the point (2,36).

i.e. we will put the input value '2' in the following given functions and check which gives the output value as '36'.

1)

`f(x)=4* 3^x`

now we put x=2.

`f(2)=4* 3^2\\\\f(2)=4* 9\\\\f(2)=36`

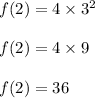
hence option 1 is correct.

2)

`f(x)=4* x^3`

Now we put x=2.

`f(2)=4* 2^3\\\\f(2)=4* 8\\\\f(2)=32`

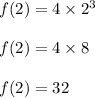
Hence, option 2 is incorrect.

3)

`f(x)=6* 3^x`

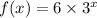
Now we put x=2

`f(2)=6* 3^2\\\\f(2)=6* 9\\\\f(x)=54`

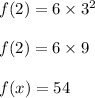
Hence, option 3 is incorrect.

4)

`f(x)=6* x^3`

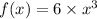
Now we put x=2.

`f(2)=6* 2^3\\\\f(2)=6* 8\\\\f(2)=48`

Hence, option 4 is incorrect.

Hence, option 1) is correct.

i.e. The exponential function that passes through (2,36) is:

`f(x)=4* 3^x`