Question

In ΔABC, m∠CAB = 60° and AD is angle bisector with D∈ BC and AD = 8 ft. Find the distances from D to the sides of the triangle.

Answer 1

4 ft.

Explanation:

Given: In ΔABC, m∠CAB = 60° and AD is angle bisector with D∈ BC and AD = 8 ft.

Draw a diagram according to the given information, the draw altitude on each side from point D.

We need to find the length of the altitude.

AD is an angle bisector, So, AD divides the angle m∠CAB = 60° in two equal parts.

`\angle EAD=\angle FAD=30^(\circ)`

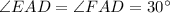
In a right angle triangle,

`\sin \theta = (opposite)/(hypotenuse)`

In triangle ADE,

`\sin EAD = (DE)/(AD)`

`\sin (30^(\circ)) = (DE)/(8)`

`(1)/(2) = (DE)/(8)`

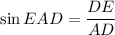
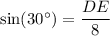
Multiply both sides by 8.

`4 = DE`

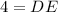
Therefore, the value of DE is 4 ft.

In triangle ADE and ADF,

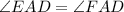`\angle EAD=\angle FAD` (AD is angle bisector)

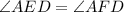`\angle AED=\angle AFD` (Right angles)

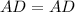`AD=AD` (Reflexive property)

By AAS triangle ADE and ADF are congruent. The corresponding parts of congruent triangles are congruent.

`DE\cong DF`

`DE=D F=4ft`

Therefore, the distances from D to the sides of the triangle is 4 ft.

Answer 2

The distances from D to the sides of the triangle is 4 ft.

Explanation:

Given information: In ΔABC, ∠CAB = 60° and AD is angle bisector with D∈ BC and AD = 8 ft.

Since AD is angle bisector and ∠CAB = 60°, therefore

`\angle BAD=\angle CAD=30^(\circ)`

Draw perpendicular on AB and AC form D.

`\sin \theta=(perpendicular)/(hypotenuse)`

In triangle ADE,

`\sin 30=(DE)/(8)`

`(1)/(2)=(DE)/(8)`

Multiply both sides by 8.

`4=DE`

In triangle ADF,

`\sin 30=(DF)/(8)`

`(1)/(2)=(DF)/(8)`

Multiply both sides by 8.

`4=DF`

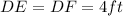
Therefore the distances from D to the sides of the triangle is 4 ft.