Answer:
The perimeter of ΔABC is 43 units
Explanation:
An illustrative diagram is shown in the attachment below.
To find the perimeter of the triangle, we will first determine the length of the unknown sides.
First, we can determine /BC/ using the Sine rule
From Sine rule
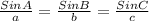
∴
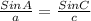
In the diagram,
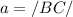 and
and
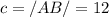
m∠A=60° and m∠C=45°
∴
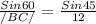
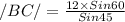

To find /AC/, will first determine m∠B
m∠A + m∠B + m∠C = 180° (Sum of angles in a triangle)
60° +m∠B + 45° = 180°
m∠B + 105° = 180°
m∠B = 180° - 105°
m∠B = 75°
Also, using the sine rule
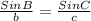
From the diagram,



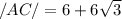
Now,
The perimeter of ΔABC = /AB/ + /BC/ + /AC/
=
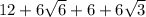
= 43.09 units
≅ 43 units
Hence, the perimeter of ΔABC is 43 units.