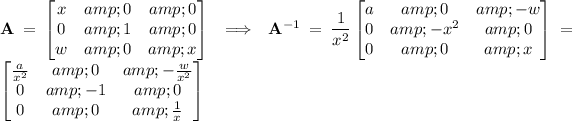Inverse this matrix \left[\begin{array}{ccc}x&0&0\\0&1&0\\w&0&x\end{array}\right]

Question

Inverse this matrix


`\left[\begin{array}{ccc}x&0&0\\0&1&0\\w&0&x\end{array}\right]`

Answer 1

In order for the inverse to exist, the matrix cannot be singular, so we need to first examine the conditions for existence of the inverse.

Compute the determinant. The easiest way might be a cofactor expansion along either the first row or third column; I'll do the first.


`\begin{vmatrix}x&0&0\\0&1&0\\w&0&x\end{vmatrix}=x\begin{vmatrix}1&0\\0&x\end{vmatrix}=x^2`

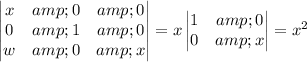
The matrix is then singular whenever
`x\\eq0`.

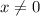
With this in mind, compute the inverse.


`\mathbf A=\begin{bmatrix}x&0&0\\0&1&0\\w&0&x\end{bmatrix}\implies\mathbf A^(-1)=\frac1{x^2}\begin{bmatrix}a&0&-w\\0&-x^2&0\\0&0&x\end{bmatrix}=\begin{bmatrix}\frac a{x^2}&0&-\frac w{x^2}\\0&-1&0\\0&0&\frac1x\end{bmatrix}`