Answer:
Conner's work is right.
Explanation:
The given expression is
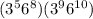
To solve this products, we need to use power properties, like the one below
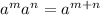
In words, the product between powers which have the same base, results in the same base and the exponent is the sum of the first two.
So, if we apply this property, we have
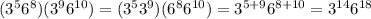
Now, if we compare Conner's work and Jana's work, you will observe that Conner is right, because he applied the right property of powers to simplify the expression.
Therefore, Conner's work is right.