Answer:
The simplified form is
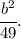
Explanation:
The goal of the exercise is to apply exponent properties. On this case we need to distribute the exponent to each expression of the fraction, that is to the numerator and to the denominator, using the distribution exponent property.
![\[\left( \cfrac{a}{b}\right)^n= \cfrac{a^n}{b^n}\]](https://img.qammunity.org/2018/formulas/mathematics/high-school/ydqrde9lvnl60wt91umm7yloo7bmlg6nxj.png)
In a general way we can always distribute exponents over multiplication or division.
Simplifying using exponent distribution property.
Applying the property to the exercise give us
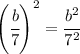
Lastly we know that
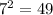 so we get
so we get
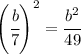
And that is the simplified form of the given expression.