Question

Somebody please help so I can pass, please

Rewrite the following equation in the form y = a(x - h)2 + k. Then, determine the x-coordinate of the minimum.

y=2x^2 - 32x + 56

The rewritten equation is y = ____ (x - _____ )2 + ____ .
The x-coordinate of the minimum is _____

Answer 1

y = 2 (x - 8 )2 + (-72)) .

The x-coordinate of the minimum is 8.

Explanation:

I just took this test on plato and I got it correct.

Answer 2

First, we are going to find the vertex of our quadratic. Remember that to find the vertex
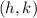
`(h,k)` of a quadratic equation of the form
`y=a x^(2) +bx+c`, we use the vertex formula
`h= (-b)/(2a)`, and then, we evaluate our equation at
`h` to find
`k`.

We now from our quadratic that
`a=2` and
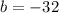
`b=-32`, so lets use our formula:

`h= (-b)/(2a)`

`h= (-(-32))/(2(2))`

`h= (32)/(4)`

`h=8`
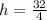
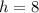
Now we can evaluate our quadratic at 8 to find
`k`:

`k=2(8)^2-32(8)+56`

`k=2(64)-256+56`

`k=128-200`

`k=-72`
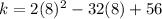
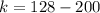
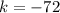
So the vertex of our function is (8,-72)

Next, we are going to use the vertex to rewrite our quadratic equation:

`y=a(x-h)^2+k`

`y=2(x-8)^2+(-72)`

`y=2(x-8)^2-72`
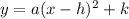
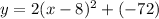
The x-coordinate of the minimum will be the x-coordinate of the vertex; in other words: 8.

We can conclude that:
The rewritten equation is
`y=2(x-8)^2-72`
The x-coordinate of the minimum is 8