Question

An algebra test contains 38 problems. Some of the problems are worth 2 points each. The rest of the questions are worth 3 points each. A perfect score is 100 points.

How many problems are worth 2 points? How many problems are worth 3 points?

Answer 1

Total questions in the test = 38

Let 2 points questions be = x

Let 3 points questions be = y

As total questions are 38, so

`x+y=38`

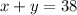
From here, we can derive x as:
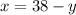`x=38-y` ...... (i)

As given, few questions are 2 marks each and rest 3 marks each and perfect square is 100, so we get,

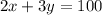`2x+3y=100` .......(ii)

Put the value of y from (i) in (ii)

`2(38-y)+3y=100`

`76-2y+3y=100`

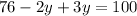
y=24

Putting y in equation (i), we get

`x=38-24`

x=14

Hence, 2 points questions are = 14

3 points questions are = 24

Answer 2

Let 'x' be the problems worth 2 points.

Let 'y' be the problems worth 3 points.

Since, there are 38 total problems.

So,
`x+y =38` (equation 1)

x = 38-y

Since, a perfect score is 100 points.

So,
`2x+3y = 100` (equation 2)

Substituting the value of 'x', we get

`2(38-y)+3y=100`

`76-2y+3y=100`

`76+y = 100`

y = 24

x+y = 38

x = 38-24 = 14

So, 14 problems are worth 2 points and 24 problems are worth 3 points.