Question

What is the determinant of the coefficient matrix of the system

Answer 1

The determinant is 0

EXPLANATION (METHOD 1)
This method involves expanding along any column.


For an n×n matrix A, the determinant of A, det(A), can be obtained by expanding along the kth column:

`\det(A) = a_(1k) C_(1k) + a_(2k) C_(2k) + \ldots + a_(nk) C_(nk)`

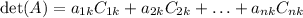
where
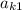`a_(k1)` is the entry of A in the kth row, 1st column,
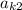`a_(k2)` is the entry of A in the kth row, 2nd column, etc., and
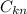`C_(kn)` is the kn cofactor of A, defined as
`C_(kn) = (-1)^(k+n) M_(kn)`.

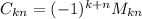But we do not need to care about the cofactors as all the 2nd column entries are

a₁₂ = a₂₂ = a₃₂ = 0

We would end up with

`\begin{aligned} \det\left(\begin{bmatrix} \bf -3 & \bf 0 & \bf -2\\ 9 & 0 & 5 \\ 6 & 0 & -12 \end{bmatrix}\right) &= (0) C_(12) + (0)C_(22) + (0)C_(32) \\ &= 0 \end{aligned}`

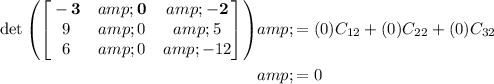
EXPLANATION (METHOD 2)|
This method involves expanding along a row

For an n×n matrix A, the determinant of A, det(A), can be obtained by expanding along the kth row:

`\det(A) = a_(k1) C_(k1) + a_(k2) C_(k2) + \ldots + a_(kn) C_(kn)`

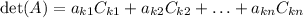
where
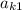`a_(k1)` is the entry of A in the kth row, 1st column,
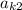`a_(k2)` is the entry of A in the kth row, 2nd column, etc., and
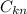`C_(kn)` is the kn cofactor of A, defined as
`C_(kn) = (-1)^(k+n) M_(kn)`.

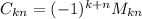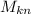`M_(kn)` is the kn minor, obtained by getting the determinant of the matrix which is the matrix A with row k and column n deleted.

Applying this here, we can expand along the 1st row.
For convenience, let G be the coefficient matrix of this question, which is

`image`

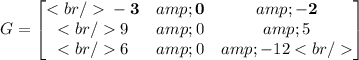
with the first row bolded.

The determinant is therefore

`image`

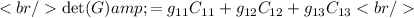
Note that g₁₁ is the matrix element of G that is in the 1st row, 1st column, g₁₂ is the matrix element of G that is in the 1st row, 2nd column, etc. Then we have

`image`

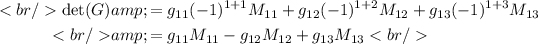
M₁₁ is the determinant of the matrix that is matrix G with row 1 and column 1 removed. The bold entires are the row and the column we delete.

The determinant of a 2×2 matrix is

`\det\left( \begin{bmatrix} a & b \\ c& d \end{bmatrix} \right) = ad-bc`

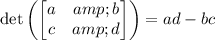
so it follows that

Applying the same for M₁₂ and M₁₃, we have

and

so therefore

`image`

Answer 2

`\left[\begin{array}{ccc}-3&0&-2\\9&0&5\\6&0&-12\end{array}\right] \\D(system)= |-3|\left[\begin{array}{ccc}0&5\\0&-12\\\end{array}\right]-0 \left[\begin{array}{ccc}9&5\\6&-12\\\end{array}\right] +|-2| \left[\begin{array}{ccc}9&0\\6&0\\\end{array}\right] \\=3*0-0+0=0\\ determinant of system is 0`