Question

The length of an aluminum wire is quadrupled and the radius is doubled. By which factor does the resistance change?

Answer 1

The resistance of a conductive wire is given by:

`R= (\rho L)/(A)`
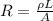
where

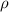
`\rho` is the material resistivity

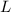
`L` is the wire length

`A` is the cross-sectional area of the wire

The length of the wire is quadrupled, so if we call L the original length and L' the new length, we can write

`L'=4 L`

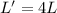
Similarly, the radius of the wire is doubled (r'=2r), so the new area is

`A'= \pi (r')^2 = \pi (2r)^2 = 4 \pi r^2 = 4A`

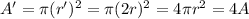
And if we substitute into the equation, we find that the new resistance of the wire is

`R'= (\rho L')/(A')= (\rho (4L))/(4 A') = (\rho L)/(A)=R`
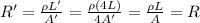
Therefore, R=R': this means that the resistance of the wire did not change.