Question

A special box designed to hold an antique artifact is shaped like a triangular prism the surface area of the box is 421.2 square inches the height of the base triangle is 7.8 inches and each side of the base triangle is 9 inches long what is the height of the box?

Answer 1

the answer is 15.9 inches

Answer 2

As we can see the base of the triangular prism is an equilateral triangle with all sides equal to 9 inches. Let us represent this by
`b=9`

It is also given that the height of the equilateral triangle is 7.8 inches. Let us represent this by
`h=7.8`

Therefore, the area of one triangle of the base of the triangular pyramid is:

`Area=(1)/(2)* b* h=(1)/(2)* 9* 7.8=35.1`

Thus, the area of the two triangles that make the bases of the triangular prism are:

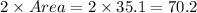`2* Area=2* 35.1=70.2`.........(Equation 1)

Now, the area of the three rectangular sides of the triangular prism can be calculated as:

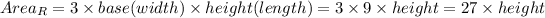`Area_R=3* base(width)* height (length)=3* 9 * height=27* height`........(Equation 2)

We have been given the total surface area of the triangular prism to be 421.2 squared inches and we know that it is the sum of the surface areas of the triangular bases and the rectangular sides. Thus, the total surface area will be the sum of (equation 1) and (equation 2) and will equal 421.2.

Therefore, we have:

`70.2+27* height=421.2`

Thus,
`27* height=421.2-70.2=351`

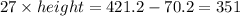
Therefore,
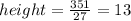`height=(351)/(27)=13` inches.