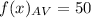Question

It takes Matt 20 months to save 1,000. Write an equation that models the average number of dollars, x, Matt saves each month.

Answer 1

To solve this we are going to use the slope formula:
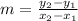
`m= (y_(2)-y_(1))/(x_(2)-x_(1) )`, and the point slope formula:
`y-y_(1)=m(x-x_(1))`

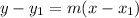
For our problem we can infer that prior to the 20 months period of saving, he didn't have any savings at all. So our first point
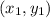
`(x_(1),y_(1))` will be (0,0). We know for our problem that after 20 month he saved 1000, so our second point
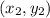
`(x_(2),y_(2))` will be (20,1000).

Now that we have our points, we can use our slope formula to find
`m`:

`m= (y_(2)-y_(1))/(x_(2)-x_(1) )`

`m= (1000-0)/(20-0)`

`m= (1000)/(20)`

`m=50`

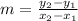
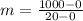
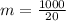
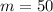
Now that we have our slope, we can use our point slope formula:

`y-y_(1)=m(x-x_(1))`

`y-0=50x-0`

`y=50x`
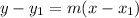
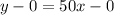
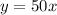
Remember that
`y` and
`f(x)` are equivalent, so:

`f(x)=50x`

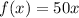
Finally, to find the average number of dollars Matt saves each month, we are going to find the average function. To do that we are going to divide our function
`f(x)` by
`x`:

`f(x)_(AV)= (f(x))/(x)`

`f(x)_(AV)= (50x)/(x)`

`f(x)_(AV)=50`

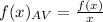
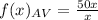
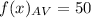
We can conclude that the function that models the average number of dollars, x, Matt saves each month is
`f(x)_(AV)=50`