Question

What are the roots of this function? f(x) = x2 – 8x + 12

A) {2, 6}
B) {8, 12}
C) {-3, -4}
D) {-4, -4}

Answer 1

Option A is correct.

the root of the given function is, {2, 6}

Explanation:

Given the function:
`f(x) = x^2-8x +12`

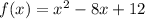
To find the root of the given function;

Set f(x) = 0

⇒
`x^2-8x+12 =0`

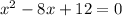
In the Quadratic Factorization using Splitting of Middle Term which is x term is the sum of two factors and product equal to last term.

Step 1. Find the product of 1st term and the last.

Product =
`1 * 12 =12`

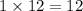
Step 2. Find the factors of 12 in such way that addition or subtraction of that factors is the middle term, i.e -8x(Splitting of middle term)

Factor =
`-6 \text{and} -2`

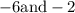
Therefore, -6-2= -8

Step 3. Group the terms to form pairs:

`x^2-6x-2x+12 =0`

`x(x-6)-2(x-6) =0`

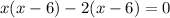
(x-6)(x-2) = 0

By zero product property ; we have

⇒x -6 = 0 and x -2 = 0

⇒x =6 and x = 2

Therefore, the roots of the function
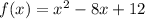`f(x) = x^2-8x +12` is, 2 and 6