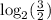Question

Choose the single logarithmic expression that is equivalent to the one shown. log2 6 + log2 2 − log2 8

Options are:

a) log2 (2/3)
b) log2 1
c) log2 (3/2)
d) log2 4

Answer 1

Option c is correct

`\log_2 ((3)/(2))`

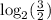
Explanation:

Using the logarithmic rules:

`\log_b (mn) = \log_b m+ \log_b n`

`\log_b (m)/(n) = (\log_b m)/(\log_b n)`

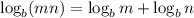
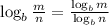
Given the expression:

`\log_2 6 + \log_2 2 - \log_2 8`

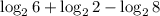
Apply the logarithmic rules:

`\log_2 (6 \cdot 2)-\log_2 8`

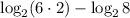
Simplify:

`\log_2 12 -\log_2 8`

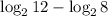
Apply the logarithmic rules we have;

`\log_2 (12)/(8) = \log_2 ((3)/(2))`

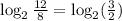
Therefore, the single logarithmic expression that is equivalent to the one shown
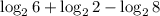`\log_2 6 + \log_2 2 - \log_2 8` is,
`\log_2 ((3)/(2))`

Answer 2

To simplify the logarithm function we shall have:
log2 6+ log2 2 -log2 8
but from the laws of logarithm we can simplify the above to
log2 [(6×2)/8]
log2 3/2
Answer: C] log2 (3/2)