Question

The manager of a warehouse would like to know how many errors are made when a product’s serial number is read by a bar-code reader. Six samples are collected of the number of scanning errors: 36, 14, 21, 39, 11, and 2 errors, per 1,000 scans each.

1A.] What is the mean and standard deviation for these six samples?
2A.] What number of errors is made by all scans, based on these six samples?

Just to be sure, the manager has six more samples taken:
33, 45, 34, 17, 1, and 29 errors, per 1,000 scans each
1B.] How do the mean and standard deviation change, based on all 12 samples?
2B.] How reasonable is it to expect that the small sample represents larger samples?

Answer 1

1A. 20.5

2A. 14.54

1B. 14.625

2B. quite good reasonable

Explanation:

Mean is used to measure central tendency (i.e. representative of data) and standard deviation is use to measure dispersion of data. The formula use to calculate mean and variance is :

`Mean(bar{x}) = (Sum of all the observations)/(Total number of observation)`

`Standard deviation(\sigma) = \sqrt{(1)/(n) \sum_(i=1)^(n)(x_(i)-\bar{x})^2}`

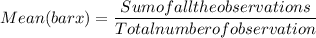
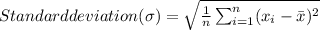
1A. Mean of six sample =

`= (Sum of all the observations)/(Total number of observation)`

⇒
`(36+14+21+39+11+2)/(6)`

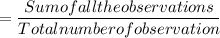
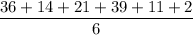
⇒ Mean = 20.5

Standard deviation of six sample =

`= \sqrt{(1)/(6)[ (36-20.5)^2+(14-20.5)^2+(21-20.5)^2+(39-20.5)^2+(11-20.5)^2+(2-20.5)^2}]`

⇒ σ = 14.54

2A. Total number of error = 36 + 14 + 21 + 39 + 11 + 2 = 123

Total number of error made by all scans is 123 error per 6000 scans.

1B. Mean of all 12 samples is:

`= (Sum of all the observations)/(Total number of observation)`

⇒
`(36+14+21+39+11+2+33+45+34+17+1+29)/(12)`

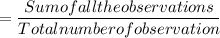
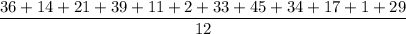
⇒ Mean = 23.5

Standard deviation of all 12 samples =

⇒ σ = 14.625

2B. Taking small sample instead of large sample can be quite risky sometimes as larger sample give us more accurate result than small sample.

But here we can take a small sample because the mean of both the size of the sample is near about.