Question

Describe the pattern in each sequence. Then find the next two terms of the sequence

Answer 1

The given sequences are

`21, 16, 11, 6, 1, -4...\\-3, 5, 13, 21, 29, 37...\\72, 44, 16, -12, -40, -68...`

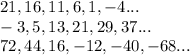
The first sequence is decreasing by a difference of 5, that is

`21-5=16\\16-5=11\\11-5=6\\6-5=1\\1-5=-4\\-4-5=-9\\-9-5=-14`

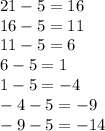
So, the next two terms are -9 and -14.

The second sequence is increasing by a difference of 8, that is

`-3+8=5\\5+8=13\\13+8=21\\21+8=29\\29+8=37\\37+8=45\\45+8=53`

So, the next two terms are 45 and 53

The third and last sequence is decreasing by a difference of 28, that is

`72-28=44\\44-28=16\\16-28=-12\\-12-28=-40\\-40-28=-68\\-68-28=-96\\-96-28=-124`

So, the next two terms of this sequence are -96 and -124.

Answer 2

General Arithmetic Progression:


`\boxed { \boxed {T_n= a_1 + d(n - 1)}}`


21 , 16 , 11 , 6 , 1 , -4


`a_1 = 21, d = -5`


`T_n = 21 -5(n - 1)`


`T_n = 21 -5n + 1`


`T_n = 22 -5n`


`\boxed { \boxed {\text {Answer: } T_n = 22 -5n }}`


-3, 5, 13, 21, 29, 39


`a_1 = -3, d = 8`


`T_n = -3 + 8(n - 1)`


`T_n = -3 + 8n - 8`


`T_n = 8n - 11`


`\boxed { \boxed {\text {Answer: } T_n = 8n - 11}}`


44, 16, -12, -40, -68


`a_1 = 44, d = -28`


`T_n = 44 - 28(n - 1)`


`T_n = 44 - 28n + 28`


`T_n = 72 -28n`


`\boxed { \boxed {\text {Answer: } T_n = 72 - 28n}}`