Question

Solve the following system. y = (1/2)x 2 + 2x - 1 and 3x - y = 1 The solutions are ( )and ( ) (remember to include the commas)

Answer 1

`\begin{cases}y=(1)/(2)x+2x-1\\3x-y=1\end{cases}\\\\\\ \begin{cases}y=(5)/(2)x-1\3x-y=1\end{cases}\\\\\\ 3x-\left((5)/(2)x-1\right)=1\\\\3x-(5)/(2)x+1=1\\\\ 3x-(5)/(2)x=0\\\\(x)/(2)=0\\\\x=0\\\\3*0-y=1\\0-y=1\\y=-1\\\\\boxed{(x,y)=(0,-1)}`

The solutions are (0) and (-1)

Answer 2

The points satisfying the solution is (2,5) and (0,-1).

Explanation:

Given :
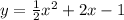`y=(1)/(2)x^2+2x-1` and
`3x-y=1`

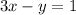
To solve : The given system of equations ?

Solution :

Let,

`y=(1)/(2)x^2+2x-1` .....[1]

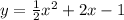`3x-y=1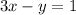` ......[2]

Now, using substitution method,

Substitute y from [1] into [2]

`3x-((1)/(2)x^2+2x-1)=1`

`3x-(1)/(2)x^2-2x+1=1`

`x-(1)/(2)x^2=0`

`2-x=0`

`x=2`

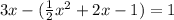
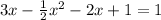
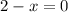
Now, substitute the value of x into [2]

`3(2)-y=1`

`6-y=1`

`y=5`

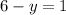
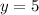
Therefore, One of the solution is (2,5)

Similar way we can substitute [2] into [1] we get another solution (0,-1).

So, for the solutions we can also graph the equations and the intersecting points are the solution of the graph.

Refer the attached figure below.

The points satisfying the solution is (2,5) and (0,-1).