Question

PLEASE HELP URGENT!!

Use graphs and tables to find the limit and identify any vertical asymptotes of the function. limit of 1 divided by the quantity x minus 1 squared as x approaches 1.

Answer 1

`\lim_(x \to\ 1)(1)/((x-1)^2)=\infty`

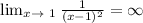
vertical asymptote at x=1

Explanation:

`\lim_(x \to\ 1)(1)/((x-1)^2)`

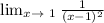
First we find out limit approaches from right

`\lim_(x \to\ 1^+)(1)/((x-1)^2)=\infty`

BEcause the denominator is a positive quantity because it has square

we find out limit approaches from right

`\lim_(x \to\ 1^-)(1)/((x-1)^2)=\infty`

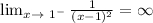
so limit is infinity

`\lim_(x \to\ 1)(1)/((x-1)^2)=\infty`

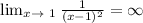
To find out vertical asymotote , we take the denomintor and set it =0

(x-1)^2=0

Take square on both sides

(x-1) = 0

add 1 on both sides

x=1

So vertical asymptote at x=1