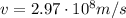Question

An object has a relativistic momentum that is 7.1 times greater than its classical momentum. What is its speed? Express the answer using two significant figures.

Answer 1

The relativistic momentum of an object is given by

`p_r = \gamma m_0 v`
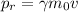
where

`\gamma= \frac{1}{\sqrt{1- (v^2)/(c^2) }}` is the relativistic factor

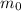
`m_0` is the rest mass of the object
v is the speed of the object
c is the speed of light

The classical momentum is given by

`p_c = m_0 v`

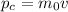
The problem says that the ratio between the relativistic and classical momentum of the object is 7.1, so

`7.1 = (p_r)/(p_c)= (\gamma m_0 v)/(m_0 v) = \gamma`
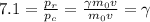
Therefore,
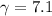
`\gamma=7.1`, and we can use the definition of
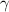
`\gamma` to find the object's speed:

`\frac{1}{ \sqrt{1- (v^2)/(c^2) } }=7.1`
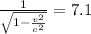
Solving,

`v= \sqrt{1- (1)/((7.1)^2) } c`
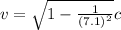
And by using
`c=3 \cdot 10^8 m/s`, we find the velocity of the object:

`v=2.97 \cdot 10^8 m/s`