Question

This is a special right triangle, what is the missing side length?

Answer 1

I would say 90 but I could be wrong.

Good Luck!!

Answer 2

The answer is: "x =
`(4 √(3) )/(3)` ." ;

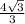
AND: "y =
`(4 √(3) )/(3)` ."
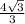
_______________________________________________________Step-by-step explanation:______________________________________________________The sides of a "45-45-90" (right triangle) are: "a", "a" ; and "a√2" .

Note that: "a√2" is the hypotenuse length— and the other 2 (TWO) sides of the triangle are of equal length— {since: "a = a" .}._______________________________________________________
As such: "x = y" ; and the hypotenuse, "x√2", equals:
"
`(4 √(6) )/(3)` " .
__________________________________________________
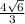
Note: The Pythagorean theorem (for the side lengths of right triangles):

→ " a² + b² = c² ;

in which: "c = the hypotenuse length" ;
"a = one of the other side lengths"
"b = the remaining side length" .
____________________________________________________
Note that: "x = y" ;

so: " x² + x² = 2x " ;

2x² = x√2 ;

2x² = c² ; in which "c" is the hypotenuse; Solve for "x" and "y" ; Since "x = y" ; solve for "x" ;

2x² = c² ;

→ Given (from image attached); " c =
`(4 √(6) )/(3)` " .

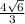
→ c² = (
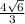
`(4 √(6) )/(3)` )² ;

=
`((4 √(6))^2 )/(3 ^(2) )` ;

=
`(4 ^(2)( √(6) ) ^(2) )/(3 ^(2) )` ;

=
`((16*6))/(9)` ;

=
`(32)/(3)` ;
____________________________________________________
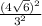
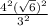
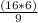
→ 2x² =
`(32)/(3)`

Divide each side of the equation by "2" ;

2x² / 2 =
`(32)/(3)`) ÷ 2 ;


x² =
`(32)/(3) * (1)/(2)` ;

Note: The "32" cancels out to "16"; and the "2" cancels out to "1" ;

→ {since: "32 ÷ 2 = 16" ; and since: "2 ÷ 2 = 1 " } l

And we have;

x² =
→ ⁺√(x²) = ⁺√((16)/(3)) ;

→ x = ⁺\frac({√16}{√3}) = [tex] (4)/( √(3) ) " src="
`image`
→ Multiply by "
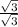
`( √(3) )/( √(3) )`" ; to eliminate the "√3" in the "denominator" ;

→
`(4)/( √(3) )` *
`( √(3) )/( √(3) )` ;

=
`(4)/( √(3) )` ÷
`( √(3) )/( √(3) )` ;

= "
`(4 √(3) )/(3)` " .
_____________________________________________________
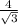
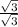
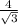
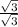
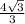
The answer is: " x =
`(4 √(3) )/(3)` ." ;

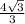
AND: " y =
`(4 √(3) )/(3)` ."
_____________________________________________________

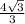
Does "x√2" = the hypotenuse length shown?

that is: Does "x√2" = "
`(4 √(6) )/(3)`" ?

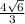
Note: " x =
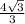
`(4 √(3) )/(3)` " ; (from our calculated answer) .
_____________________________________________________
→ Multiply this value by "√2" ; and see if we get the same values as the given hypotenuse:

→
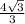
`(4 √(3) )/(3)` * √2 ;

=
`(4 √(3)* √(2) )/(3)` ?? ;

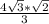
→ Note: "√3 * √2 = √(3 * 2) = √6 " ;
_________________________________________

→
`(4 √(3)* √(2) )/(3)` ;

=
`(4 √(6) )/(3)` ;

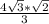
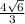
→ which is the value of the hypotenuse shown in the figure!
Yes; the answer does make sense!
_________________________________________________