Question

Can someone please check my answer fast?

The function g is defined by g(x) = x+6 over/ 2x+5

Find g(x+5)

MY ANSWER : g+11 over/ 2x+15

Answer 1

Your answer was: "g+11 over/ 2x+15 " .
____________________________________________________
Your answer was "incorrect —but almost correct" !

Instead of "(g + 11)" for the "numerator" ; you should have put: "(x + 11)" .

As a matter of technicality, you could have/should have stated:
________________________________________________________

{
`x \\eq - 7.5` } ; {
`x \\eq -2.5` }.
________________________________________________________
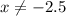
→ {but this would depend on the context — and/or the requirements of the course/instructor.}. Good job!
________________________________________________________

Step-by-step explanation:
________________________________________________________

Given: g(x) =
`((x+6))/((2x + 5))` ;

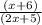
Find: g(x+5) .

To do so, we plug in "(x+5)" for all values of "x" in the equation; & solve:
________________________________________________________
Start with the "numerator": "(x + 6)" :

→ (x + 5 + 6) = x + 11 ;
__________________________________
Then, examine the "denominator" : "(2x + 5)"

→ 2(x+5) + 5 ;

→ 2(x + 5) = 2*x + 2*5 = 2x + 10 ;


→ 2(x+5) + 5 =

2x + 10 + 5 ;

= 2x + 15 ;
________________________________________________________

→ g(x + 5) =
`(x+11)/(2x +15)` .

________________________________________________________
Note that the "denominator" cannot equal "0" ;
since one cannot "divide by "0" ;
_______________________________________________________
So, given the denominator: "2x + 15" ;

→ at what value for "x" does the denominator, "2x + 15" , equal "0" ?

→ 2x + 15 = 0 ;

Subtract "15" from each side of the equation:

→ 2x + 15 - 15 = 0 - 15 ;

to get:

→ 2x = -15 ;

Divide EACH SIDE of the equation by "2" ;
To isolate "x" on one side of the equation; & to solve for "x" ;

→ 2x / 2 = -15 / 2 ;

to get:

→ x = - 7. 5 ;
Your answer was: "g+11 over/ 2x+15 " .
____________________________________________________
Your answer was "incorrect —but almost correct" !

Instead of "(g + 11)" for the "numerator" ; you should have put: "(x + 11)" .

As a matter of technicality, you could have/should have stated:
________________________________________________________

{
`x \\eq - 7.5` } ; {
`x \\eq -2.5` }.
________________________________________________________
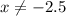
→ {but this would depend on the context — and/or the requirements of the course/instructor.}. Good job!
________________________________________________________
So; "
`x \\eq - 7.5` " .
________________________________________________________
Now, examine the "denominator" from the original equation:
________________________________________________________
→ "(2x + 5)" ;

→ At what value for "x" does the 'denominator' equal "0" ?

→ 2x + 5 = 0 ;

Subtract "5" from each side of the equation:

→ 2x + 5 - 5 = 0 - 5 ;

to get:

→ 2x = -5 ;

Divide each side of the equation by "2" ;
to isolate "x" on one side of the equation; & to solve for "x" ;

→ 2x / 2 = -5 / 2 ;

→ x = -2.5 ;

→ So; "
`x \\eq -2.5` " .
____________________________________________________
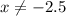
The correct answer is:
____________________________________________________
→ g(x + 5) =
`(x+11)/(2x +15)` ;

{
`x \\eq - 7.5` } ; {
`x \\eq -2.5` }.
____________________________________________________

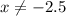
→ Your answer was: "g+11 over/ 2x+15 " .
____________________________________________________
Your answer was "incorrect —but almost correct" !

Instead of "(g + 11)" for the "numerator" ; you should have put: "(x + 11)" .

As a matter of technicality, you could have/should have stated:
________________________________________________________

{
`x \\eq - 7.5` } ; {
`x \\eq -2.5` }.
________________________________________________________
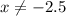→ {but this would depend on the context — and/or the requirements of the course/instructor.}. Good job!
________________________________________________________