Question

Compare the functions below:

f(x) = −3 sin(x − π) + 2 g(x)

x y
0 8
1 3
2 0
3 −1
4 0
5 3
6 8
h(x) = (x + 7)2 − 1


Which function has the smallest minimum?
f(x)
g(x)
h(x)
All three functions have the same minimum value.

Answer 1

We have been given 3 functions and we are asked to determine which of these functions has lowest minimum value.

Let us see the minimum value of each function one by one.

Our first function
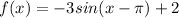`f(x)=-3sin(x-\pi)+2`. We know that range of sin function oscillates between -1 to 1.

The minimum value of the function will occur when value of sine is maximum. Let us see by substituting sin's value 1 in our function.

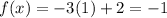`f(x)=-3(1)+2=-1`. So we get -1 as minimum value for f(x).

Our second function is g(x) and we have been given a table of values of g(x). On looking at this table we can see that g(x) also has a minimum value of -1.

Our third function is
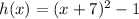`h(x)=(x+7)^(2)-1`. We can see this function is always positive except -7. Now let us evaluate this function at -7.

`h(x)=(-7+7)^(2)-1=(0)^(2)-1=-1`

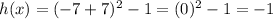
Therefore, we can see all these functions have minimum value equals to -1. So option (d) is the correct choice.