Question

The average electricity bill for Lynn’s home is $64.50 per month with a standard deviation of $8.20. In June she received a bill of only $30.00 because she was traveling for most of the month. How many standard deviations below the mean is the amount of Lynn’s electricity bill for June?

Answer 1

This bill is about 4.21 standard deviations below the mean value.

To find this, first subtract the mean from the given amount.

30 - 64.5 = -34.5

Now, divide this by 8.2, which is the amount of 1 standard deviation.

34.5 / 8.2 = 4.21

Answer 2

4.21 standard deviation below mean.

Explanation:

We have been given that the average electricity bill for Lynn’s home is $64.50 per month with a standard deviation of $8.20. In June she received a bill of only $30.00.

We will use z-score formula to solve our given problem.

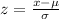`z=(x-\mu)/(\sigma)`, where,

`z=\text{z-score}`,

`x=\text{Sample-score}`,

`\mu=\text{Mean}`,

`\sigma=\text{Standard deviation}`

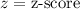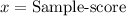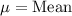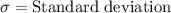
Upon substituting our given values in z-score formula we will get,

`z=(30-64.50)/(8.20)`

`z=(-34.5)/(8.20)`

`z=-4.2073170731\approx -4.21`

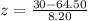
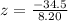
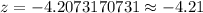
Since z-score is negative, therefore, the amount of Lynn’s electricity bill for June is approximately 4.21 standard deviations below mean.