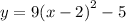Question

What is the standard form of the equation y = 1/2 (x - 4)^2 + 6

A) y= 1/2 x^2 − 8x + 22
B) y= 1/2 x^2 − 4x + 22
C) y= 1/2 x^2 − 4x + 14
D) y= 1/2 x^2 − 8x + 14

Which equation represents the quadratic parent function shifted to the left two units?
A) y=(x−2)^2
B) y=(x+2)^2
C) y=x^2 − 2
D) y=x^2 + 2

Find the equation, in vertex form, for a parabola with a vertex of (2,-5) that goes through the point (3,4).

y=.36(x+2)^2−5
y=2(x−2)^2−5
y=.75(x−2)^2−5
y=9(x−2)^2−5

Answer 1

1) The standard form for any equation is

`y = a{x}^(2) + bx + c`
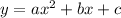
with this said we have to get the equation that they gave us into this form so we have

`y = (1)/(2) {(x - 4)}^(2) + 6`
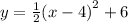
this means that the order of operations we have to follow is PEMDAS to get it to the standard form
Parentheses
Exponent
Multiplication
Division
Addition
Subtraction

`y = (1)/(2) {(x - 4)}^(2) + 6 \\ y = (1)/(2)( (x - 4) * (x - 4)) + 6 \\ y = (1)/(2) ( {x}^(2) - 4x - 4x + 16) + 6 \\ y = (1)/(2) ( {x}^(2) - 8x + 16) + 6 \\ y = (1)/(2)x - 4x + 8 + 6 \\ y = (1)/(2)x - 4x + 14`
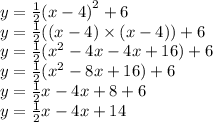
or option C in this case.

2) The quadratic parent function is

`y = {x}^(2)`
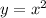
in general if you want to move the parent function to move to the left r units you will have

`y = {(x + r)}^(2)`
so in this case you will have

`y = {(x + 2)}^(2)`
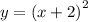
3)

The equation to find the vertex is

`y = a {(x - h)}^(2) + k`
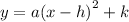
since the paranola has vertex (2,-5) we have

`y = a {(x - 2)}^(2) - 5`
to solve for a, we plug the values (3,4) into the equation and have the following


`y = a {(x - 2)}^(2) - 5 \\ 4 = a {(3 - 2)}^(2) - 5 \\ 4 = a - 5 \\ 9 = a`
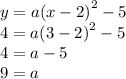
once we have the value for a, we plus it into the previous equation to get the equation of a parabola with the desired vertex and that passes through the desired point so


`y = 9 {(x - 2)}^(2) - 5`