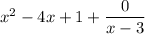Question

Rewrite the rational expression( x^3-7x^2+13x-3) / (x-3) in the form q(x) +

r(x)/b(x), and then match q(x), r(x), and b(x) to the correct expressions.
Tiles are:
x^2-7x+13
x^2-4x+1
x^3-7x^2+13x-3
x-3
-3
0
pair to
q(x) =
b(x) =
r(x) =
Please help!!

Answer 1

`q(x)=x^2-4x+1`

`b(x)=x-3`

`r(x)=0`

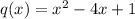
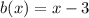
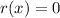
Step-by-step explanation:

The given rational expression is

`(x^3-7x^2+13x-3)/(x-3)`

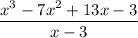
We need to write this expression as

`q(x)+(r(x))/(b(x))`

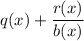
where, q(x) is quotient, r(x) is remainder and b(x) is divisor.

`b(x)=x-3`

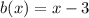
The coefficients of dividend are 1, -7, 13 and -3.

Using synthetic division, we get

3 | 1 -7 13 -3

| 3 -12 3

------------------------------------

1 -4 1 0

------------------------------------

First three elements of bottom row represents the quotient and last element of bottom row represents the remainder.

`q(x)=x^2-4x+1`

`r(x)=0`

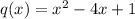
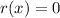
The given expression can be written as

`x^2-4x+1+(0)/(x-3)`

Answer 2

The correct answers are:
q(x) =
`x^2-4x+1`
b(x) = x-3
r(x) = 0

Step-by-step explanation:
By using synthetic division, we would get:
| 1 -7 13 -3
3 | 3 -12 3
---------------------------------
1 -4 1 0

q(x) = [1 -4 1] =
`1*x^2-4x+1`
b(x) = x - 3 (Expression with which you're dividing)
r(x) = 0 (Since the last reminder is 0)