Question

What is the slant height x of this square pyramid?

Enter your answer in the box. Express your answer in radical form.

x = ___ m

Please explain how you solved it.

Answer 1

Answer: The slant height of the given square pyramid is 2√3 m.

Step-by-step explanation: We are given to find the slant height of the square pyramid shown in the figure.

As modified in the attached figure, the pyramid consists of four congruent equilateral triangles with side length 4 m and a square base of side length 4 m.

ΔABC is one of the four triangles.

We are to find the value of x.

In ΔABC, AB = BC = CA = 4 m and AD ⊥ BC, so D will be the mid-point of BC because any altitude of an equilateral triangle divides the opposite side into two equal parts.

That is,

`BD=DC=(1)/(2)* BC=(1)/(2)*4=2.`

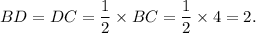
Now, from the right-angled triangle ABD, we have

`AB^2=BD^2+AD^2~~~~~\textup{[Using Pythagoras theorem]}\\\\\Rightarrow AD^2=AB^2-BD^2\\\\\Rightarrow x^2=4^2-2^2\\\\\Rightarrow x=√(16-4)\\\\\Rightarrow x=√(12)\\\\\Rightarrow x=2\sqrt3.`

Thus, the slant height of the given square pyramid is 2√3 m.